


Next: About this document ...
MATH/CSCI 2113
Assigment 1
Due Wednesday, January 16, at the beginning of class.
For each of the following problems, show your work.
- Pamela has 15 different books. In how many ways can she place
her books on two shelves so that there is at least one book on each
shelf?
- (a) In how many ways can the letters in the word VISITING be arranged?
(b) For the arrangements of part (a), hwo many have all three I's
together?
- In a social dance class, there are 12 women and 8 men. In how
many ways can the 8 men be paired with 8 of the 12 women?
- How many 4 digit integers:
- (a)
- contain all different digits?
- (b)
- do not contain the digit 5?
- (c)
- do not end with 5 or start with 1?
- (d)
- do not contain more than one 5?
- (e)
- have their digits in strictly increasing order? (So the
first digit is smaller than the second digit, etc. For example, 1356
and 2478 have their digits in increasing order.)
- Determine how many ways 20 coins can be selected from four large
containers, one filled with pennies, one with nickels, one with dimes
and one with quarters.
- In the following program,
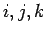 and
and  are integer
variables. Determine the value that the variable
are integer
variables. Determine the value that the variable  will have
after the segment is executed.
will have
after the segment is executed.
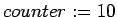
for 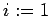 to
to 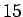 do
do
for 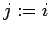 to
to 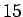 do
do
for 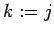 to
to 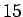 do
do
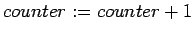



Next: About this document ...
Jeannette Janssen
2002-01-09
![]()
![]() to
to ![]() do
do
![]() to
to ![]() do
do
![]() to
to ![]() do
do
![]()