


Next: About this document ...
MATH/CSCI 2113
Assigment 4
Due Friday, February 8, at the beginning of class.
For each of the following problems, show your work.
- Give a formula for the coefficients
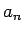 if the sequence
if the sequence
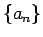 has the given generating function
has the given generating function 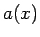 :
:
- (a)
-
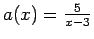
- (b)
-
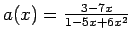 ( use partial fractions)
( use partial fractions)
- (c)
-
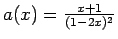
For the following problems, let 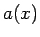 be the generating function of
the recursively defined sequence
be the generating function of
the recursively defined sequence 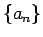 . Find an equation
satisfied by
. Find an equation
satisfied by 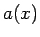 , and solve for
, and solve for 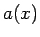 . ( You do not have to find a
direct formulat for
. ( You do not have to find a
direct formulat for 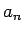 .)
.)
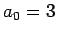 , and
, and
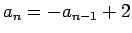 for
for 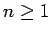 .
.
-
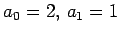 , and
, and
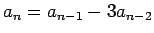 for
for 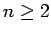 .
.
- For this problem, do the same as in the previous two, but also
find a direct formula for
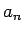 :
:
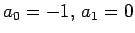 , and
, and
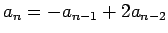
- Do Exercise 11.1.2, page 483 of the text book.
- Do Exercise 11.1.6, page 483 of the text book.
- Do Exercise 11.1.10, page 484 of the text book.
- Do Exercise 11.1.14, page 484 of the text book.
Jeannette Janssen
2002-01-30
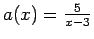
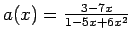 ( use partial fractions)
( use partial fractions)
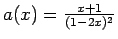
![]() be the generating function of
the recursively defined sequence
be the generating function of
the recursively defined sequence ![]() . Find an equation
satisfied by
. Find an equation
satisfied by ![]() , and solve for
, and solve for ![]() . ( You do not have to find a
direct formulat for
. ( You do not have to find a
direct formulat for ![]() .)
.)