


Next: About this document ...
MATH/CSCI 2113
Assigment 5
Due Wednesday, February 27, at the beginning of class.
For each of the following problems, show your work.
- Consider the graph
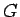 , given below. Form the adjacency
matrix for this graph, and use this matrix to compute the number of walks
of length 4 between all pairs of vertices.
, given below. Form the adjacency
matrix for this graph, and use this matrix to compute the number of walks
of length 4 between all pairs of vertices.
figure=graph3.eps, width=7cm
- Consider the directed graph of section in the text book. Form
the adjacency matrix for this graph, and use this matrix to compute
(i) the number of walks of length 3 between all pairs of vertices,
(ii) the number of common out-neighbours of each pair of vertices, and
(iii) the number of common in-neighbours of each pair of vertices.
figure=digraph4.eps, width=7cm
- If
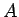 is the adjacency matrix of a graph
is the adjacency matrix of a graph 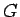 , then what do the
entries of the matrix
, then what do the
entries of the matrix 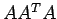 represent? Explain your answer.
represent? Explain your answer.
- Draw all graphs with vertex set
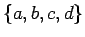 and three
edges. Indicate which of these graphs are isomorphic.
and three
edges. Indicate which of these graphs are isomorphic.
- (a) Give an example of a graph so that the graph itself and its
complement are both connected. (b) Give an example of a graph where the
graph itself is connected, and its complement has two components.
- (a) Given an example of a graph that is isomorphic to its
complement. (b) Derive a formula (in terms of
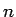 , the number of
vertices) for the number of edges in a graph that is isomorphic to its
complement. Explain your answer.
, the number of
vertices) for the number of edges in a graph that is isomorphic to its
complement. Explain your answer.
- Do problem 11.3.18 on page 504 of the text book.
- Do problem 11.5.2 on page 529 of the text book.



Next: About this document ...
Jeannette Janssen
2002-02-12