OUTPUT: A (depth-first) spanning tree
Depth-first Search
INPUT: A connected graph ![]() ,
,
![]() .
.
OUTPUT: A (depth-first) spanning tree ![]() of
of ![]() .
.
Breadth-first Search
INPUT: A connected graph ![]() ,
,
![]() .
.
OUTPUT: A (breadth-first) spanning tree ![]() of
of ![]() .
.
Vertex set:
![]() .
.
Adjacency matrix:
![\begin{displaymath}
\left[
\begin{array}{cccccccc}
0&1&1&1&0&0&0&0\\
1&0&0&1&1&...
...0&0&0\\
0&0&1&0&0&0&0&0\\
0&0&0&1&1&0&0&0
\end{array}\right]
\end{displaymath}](img19.gif)
Merge sort:
INPUT: A list ![]() of
of ![]() unordered numbers
unordered numbers
OUTPUT: A list ![]() of the same numbers in increasing order.
of the same numbers in increasing order.
A relation from set ![]() to set
to set ![]() is a subset of
is a subset of ![]() .
.
Notation: Given a relation
![]() ,
,
A relation ![]() on a set
on a set ![]() is a relation from
is a relation from ![]() to
to ![]() . Such a relation can
have the following properties (universe of the quantifiers is
. Such a relation can
have the following properties (universe of the quantifiers is ![]() ):
):
Reflexive:
Symmetric:
Antisymmetric:
Transitive:
| refl. | sym. | antis. | trans. | ||
| people | X | X | |||
| reals | X | X | |||
| reals | X | X | X | ||
| integers | X | X | X | ||
| integers | X | X | X | ||
| people | X | X | X | ||
| people | X | X | |||
| integers | |||||
| sets | X | X | X | ||
| integers | |||||
| relatively prime | X | ||||
| integers | X | X | X | ||
| have the same remainder | |||||
| bit strings | X | X | X | ||
| of length 7 | number of 1's | ||||
| web pages |
Partial order: a relation that is reflexive, antisymmetric and
transitive.
Examples:
Equivalence relation: a relation that is reflexive, symmetric and
transitive.
Examples:
A relation ![]() on a set
on a set ![]() can be represented as a directed
graph
can be represented as a directed
graph ![]() as follows:
as follows:
The vertices of ![]() are the elements of
are the elements of ![]()
The edge set
![]() .
.
A relation ![]() on a set
on a set
![]() can be represented by an
can be represented by an ![]() relation matrix
relation matrix
![]() as follows:
as follows:
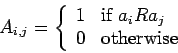
Note that the relation matrix of ![]() is the adjacency matrix of the
directed graph representing
is the adjacency matrix of the
directed graph representing ![]() .
.