Partial order: a relation that is reflexive, antisymmetric and
transitive.
Examples:
Equivalence relation: a relation that is reflexive, symmetric and
transitive.
Examples:
A relation ![]() on a set
on a set ![]() can be represented as a directed
graph
can be represented as a directed
graph ![]() as follows:
as follows:
The vertices of ![]() are the elements of
are the elements of ![]()
The edge set
![]() .
.
A relation ![]() on a set
on a set
![]() can be represented by an
can be represented by an ![]() relation matrix
relation matrix
![]() as follows:
as follows:
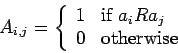
Note that the relation matrix of ![]() is the adjacency matrix of the
directed graph representing
is the adjacency matrix of the
directed graph representing ![]() .
.
Partial Orders
Given a partial order ![]() on a set
on a set ![]() :
:
An element ![]() is maximal if
is maximal if
An element ![]() is minimal if
is minimal if
An element ![]() is a greatest element if
is a greatest element if
An element ![]() is a least element if
is a least element if
Let ![]() .
.
An element ![]() is a lower bound of
is a lower bound of ![]() if
if
An element ![]() is a greatest lower bound (glb) of
is a greatest lower bound (glb) of ![]() if
if ![]() is a
lower bound of
is a
lower bound of ![]() , and for every lower bound
, and for every lower bound ![]() of
of ![]() ,
, ![]() .
.
Let ![]() .
.
An element ![]() is a upper bound of
is a upper bound of ![]() if
if
An element ![]() is a least upper bound (lub) of
is a least upper bound (lub) of ![]() if
if ![]() is an
upper bound of
is an
upper bound of ![]() , and for every upper bound
, and for every upper bound ![]() of
of ![]() ,
, ![]() .
.