Error-correcting codes

Note: all arithmetic to follow is done over ${\mathbb{Z}}_2$.

Rectangular codes

Idea: a message is a bit string of length $h\ell$. Arrange the bits of the message in a $h\times \ell$ rectangle, and add a parity check bit at the end of each row and column. This results in a code word of length $(h+1)(\ell+1)$.

To decode: find the sum of each row and column of the encoded rectangle. If exactly one row sum (of row $i$) and one column sum (of column $j$) equal 1, then an error occurred in the $i$-th row and the $j$-th column. Change this bit to decode. If more than one row sum or more than one column sum equal 1, then the information is ambiguous and decoding is not possible.

Example: take $h=2$, $\ell=3$. So the messages are all bit strings of length 6. Take for example the message $110011111$.

Arrange in rectangle and add parity bits:

1	1	0	0
0	1	1	0
1	0	1	0

So the codeword has length $3\cdot4=12$. Moreover, each codeword, when arranged in a $3\times 4$ rectangle, has all row and column sums equal to zero.

Decoding: suppose the word $111001101010$ is received. Arrange in rectangle:

1	1	1	0
0	1	1	0
1	0	1	0

The row sums are 1,0,0, respectively, and the column sums are 0,0,1,0, respectively. So only row 1 and column 3 have sum equal to 1, so we can assume that an error occurred in the first row, third column. If we correct this bit, we obtain the code word given above.

Definition: a code is linear if the following holds: if $c_1$ and $c_2$ are codewords, then $c_1+c_2$ is also a code word.

A rectangle code is a linear code.

Syndromes

Consider the rectangle code given before. In the example given above, we obtained row sums 1,0,0, and column sums 0,0,1,0. The word consisting of the row sums and column sums is called the syndrome of the received word. So for our example, the syndrome equals 1000010.

The syndrome can also be calculated directly from the received word $111001101010$, without using the rectangle. For the first bit of the syndrome (the sum of the first row), we add bits 1, 2, 3 and 4 of the received word. For the second, we add bits 5, 6, 7, and 8. For the third, we add bits 9, 10, 11, 12. For the fourth syndrome bit, which gives the sum of the first column, we add bits 1, 5 and 9. For the fifth syndrome bit, we add bits 2, 6, and 10, etc.

In general, if we receive the word $x_1x_2\dots x_{12}$, then the syndrome bits $s_1s_2\dots s_7$ are given by:

$$\begin{array}{l} s_1 = x_1+x_2+x_3+x_4\\ s_2 = x_5+x_6+x_7+... ...\\ s_6 = x_3+x_7+x_{11}\\ s_7 = x_4+x_8+x_{12}\\ \end{array}$$

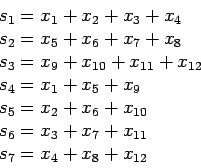
This can be written in matrix form:

$$\left[\begin{array}{cccccccccccc} 1&1&1&1&0&0&0&0&0&0&0&0\\ ... ...{c} s_1\\ s_2\\ s_3\\ s_4\\ s_5\\ s_6\\ s_7 \end{array}\right]$$

The matrix representing the parity checks is called the parity check matrix, and is usually called $H$.

Every code word has syndrome equal to the zero vector, and in fact, any word $c$ for which $Hc=0$ is a code word. Therefore, $H$ completely defines the code.

The next question: can we define other matrices $H$ that may give a better code?

Hamming codes

Hamming codes are codes that can correct one error. They are defined by their parity check matrix, which is a socalled Hamming matrix. The parity check matrix will be decoded by $H$.

First we take a closer look at the parity check matrix and its properties. An error that occurred in a code word $c$ can be represented by an error vector $e$, in the sense that the received word $x$ is the sum of the code word and the error vector: $x=c+e$. In the example given before, $x=111001101010$, $c=110001101010$, and $e=001000000000$.

Now the syndrome $s$ can be computed, as explained, by a matrix computation: $s=Hx$. But $Hx=H(c+e)=Hc+He$. Since $c$ is a code word, $Hc=0$, so we get that $s=He$. We can compute the syndrome, but how can we determine the error vector from the syndrome?

In the case on one-error-correcting codes this is easy. In this case, $e$ can always be assumed to be a vector of Hamming weight at most 1 (in other words, with at most one 1). Suppose $e$ has a 1 in the $i$-th position. Then $He$ will be exactly equal to the $i$-th column of $H$ (easy to check). So if we know the syndrome, which is equal to $He$, it is easy to determine $e$: just find out which column of $H$ is equal to the syndrome.

In the example of the rectangle code, some syndromes do not correspond to any column of $H$. Take, for example, $x=111101101010$. The syndrome is (check this!) $s=0000011$, which does not correspond to any column of $H$. So there is no code word at Hamming distance 1 from $x$, and we cannot decode $x$.

The idea for the Hamming code is to let this situation never happen. Therefore, the parity check matrix for a Hamming code with parameter $r$ will have as its columns all possible bit strings of length $r$, except for $00\dots 0$. So $H$ has $n=2^r-1$ columns and $r$ rows, and code words have $n=2^r-1$ bits, while syndromes have $r$ bits. For example, the Hamming matrix for $r=3$ is:

$$H=\left[\begin{array}{ccccccc} 1&0&1&0&1&0&1\\ 0&1&1&0&0&1&1\\ 0&0&0&1&1&1&1 \end{array}\right]$$

For example, take $x=1111111$, then $s=Hx=000$, so $x$ is a codeword. Take $x=1101111$. Then $s=Hx=110$, which is equal to the third column. So we know that the error occurred in the third bit. If $x=1100111$, then $s=111$, so the word would get decoded as $1100110$. Indeed, we see that $1100110+0000001$ and $1111111+0110000$ both give the same answer $1100111$. However, since it is more likely that one error occurs than two, the decoding makes sense.

The Hamming code consists of all code words so that $Hc=0$. This means that, in linear algebra terms, the code is the null space of the matrix $H$. It also follows from a theorem in linear algebra that the dimension of the null space equals the number of columns of $H$ (7 in our example, $n=2^r-1$ in general) minus the rank of $H$ (3 in our example, $r$ in general). So a Hamming code with parameter $r$ is a vector space of dimension $n-r$, where $n=2^r-1$. This means that the code has a basis of $n-r$ vectors, and any code word can be represented as a linear combination of the basis vector. Since we are working in ${\mathbb{Z}}_2$, the coefficients can only take values 0 and 1. So to form a linear combination of the basis vectors, we have exactly two choices for each basis vector: either include it (coefficient equals 1) or not (coefficient equals 0). So in total, there are $2^{n-r}$ possible linear combinations of the $n-r$ basis vectors, so there are $2^{n-r}$ code words.

Consider the set of words formed by a code word, and all code words at Hamming distance 1 from it, in other words, all words that can be obtained from the code word by making exactly one error. In our example, one such set consists of the code word 0000000, and the words 1000000, 0100000, 0010000, 0001000, 0000100, 0000010, 0000001. Now in order to be able to correct one error, the set of one code word must be disjoint from the set of any other code word. Each such set has size $1+n$, where $n$ is the length of the code word. Since all sets are disjoint, the union of all these sets has exactly $m(1+n)$ elements. Since there are only $2^n$ possible words of length $n$, we have that $m(1+n)\leq 2^n$, where $m$ is the number of code words.

For Hamming codes, we just saw that $m=2^{n-r}$, while $n=2^r-1$. So we have that $m(n+1)=2^{n-r}(2^r-1+1)=2^{n-r}2^r=2^n$. So we have equality; this means that the sets just described exactly fill the whole space of words of length $n$. In other words, every bit string of length $n$ is either a code word, or lies at Hamming distance 1 from a code word. So in this sense, Hamming codes are optimal; it is not possible to make a bigger code (and thus be able to send more different messages), if you are constrained to send words of length $n$, and you want to be able to correct one error.

The representation of the code as a vector space also gives us the way to encode a message. There are $2^{n-r}$ code words, so all bit strings of length $n-r$ can each receive their own code word. But, given a bit string $x=x_1\dots x_{n-r}$, how do we find the corresponding code word? For this we use the basis vectors. As argued before, the code has a basis of size $n-r$, say consisting of vectors $b_1,\dots,b_{n-r}$ (note that each of these vectors has length $n$). Then we can map the message $x$ to the code word $x_1b_1+x_2b_2+\dots +x_{n-k}b_{n-k}$. This still means we have to find a basis; this can be done with the standard methods of linear algebra, but we will omit the details here.