Generating permutations (lexicographic order)

figure=permtree.eps, width=0.8

Generating permutations

Input: $n$.
Output: all permutations of $1,2,\dots,n$, listed in lexicographic order.

1. Start with the permutation
   $s_1=1, s_2=2,\dots, s_n=n$.
2. Find the rightmost element $s_i$ so that
   $s_{i-1}<s_i$.
3. Find the smallest element $s_j$ so that
   $s_j>s_i$ and $j>i$.
4. Swap $s_i$ and $s_j$.
5. Rearrange the elements $s_{i+1}\dots s_n$ in increasing order.
6. Repeat steps 2-5 until no element $s_i$ can be found in step 2 (so all $s_i$'s are in decreasing order).

Generating permutations (minimal difference)

figure=permtree2.eps, width=0.8

Inclusion/Exclusion Principle:

For all sets $A,B,C,D$:

$$\vert A\cup B\vert=\vert A\vert+\vert B\vert-\vert A\cap B\vert$$

$$\vert A\cup B\cup C\vert=\vert A\vert+\vert B\vert+\vert C\v... ...\vert A\cap C\vert-\vert B\cap C\vert+\vert A\cap B\cap C\vert$$

$$\begin{eqnarray*} \vert A\cup B\cup C\cup D\vert&=\vert A\vert+\vert B\vert+\ver... ...ert+\vert B\cap C\cap D\vert\\ &-\vert A\cap B\cap C\cap D\vert \end{eqnarray*}$$

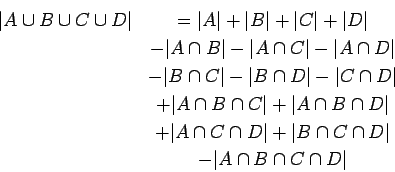
Etc.....