| Page 5a | CIRCLE Menu | MAIN MENU |
| The Pythagorean Theorem can also be used to find the equations of circles centred at any point, | 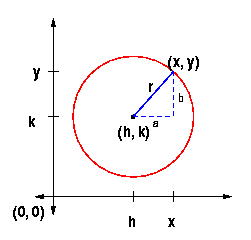 |
| The circle in Figure 1 is centred at | |
| Answer the following questions about the picture in Figure 1 to discover lengths of legs a and b in the right triangle. | |
| You will then use this information to arrive at the standard form of an equation of a circle. |
| Now we can label the dimensions of the right triangle as shown in Figure 2: | ![[TRIANGLE in CIRCLE]](images/circtrit.gif) |
| Using the Pythagorean Theorem, a2 + b2 = c2, we can derive the following equation: | |
| Notice that this is the same standard equation for a circle that we found using the distance formula. Again we see that the Distance Formula and the Pythagorean Theorem are equivalent. |