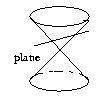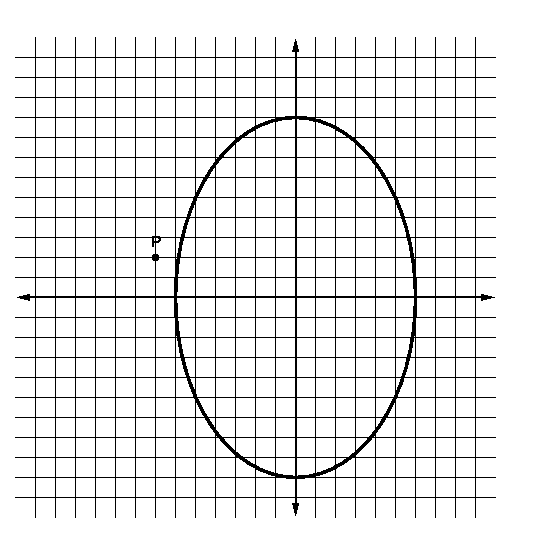Instructions:Answer all the following questions in the space provided. Simplify all answers.
- For the following standard equations, identify the centre of the ellipse and the lengths of the horizontal and vertical axes.
a) x2/ 16 + y2/ 49 = 1
| Centre: __________
Horizontal Axis: __________
Vertical Axis: ____________
b) (x - 1)2/ 4 + y2/ 25 = 1
|
Centre: __________
Horizontal Axis: __________
Vertical Axis: ____________
c) (x - 10)2/ 20 + (y + 7)2/ 144 = 1
|
Centre: __________
Horizontal Axis: __________
Vertical Axis: ____________
| | |
- An ellipse centred at the origin has a horizontal axis of length 10 and a vertical axis of length 8.
a) Sketch the graph of this ellipse on the graph paper provided.
|  |
| |
| b) Write the equation of this ellipse in standard form. | ______________________________________ |
| |
| c) Write the equation of this ellipse in general form. | ______________________________________ |
- An ellipse centred at (-3, -9) has a horizontal axis of length 2Ö5 and a vertical axis of length 16.
a) Sketch the graph of this ellipse on the graph paper provided.
|  |
| |
| b) Write the equation of this ellipse in standard form. | ______________________________________ |
| |
| c) Write the equation of this ellipse in general form. | ______________________________________ |
- Describe the effect that varying h and k in the standard equation (x - h)2/ a2 + (y - k)2/ b2 = 1 has on the graph of an ellipse by completing the following chart.
The Effect of h, k and r on the graph of (x - h)2/ a2 + (y - k)2/ b2 = 1
|
Variable |
The value of the variable decreases |
The value of the variable increases |
The value of the variable is 0. |
|---|
| h |
|
|
|
| k |
|
|
|
- Describe the effect that varying a and b in the standard equation (x - h)2/ a2 + (y - k)2/ b2 = 1 has on the graph of an ellipse by completing the following chart.
The Effect of a and b on the graph of (x - h)2/ a2 + (y - k)2/ b2 = 1
|
Value of a and b |
Effect on the graph of the ellipse |
|---|
| a > b |
|
| a < b |
|
| a = b |
|
- The equation 16x2 + y2 - 160x - 16y + 400 = 0 defines an ellipse.
a) Determine the centre of the ellipse and the lengths of its horizontal and vertical axes.
centre = |
______________ |
horizontal axis length = |
_______________
vertical axis length = | |
_______________
|
b) Sketch a picture of this ellipse on the provided graph paper.
- An ellipse is defined by the standard equation (x + 9)2/ 9 + (y + 4)2/ 36 = 1 and by the general equation 4x2 + y2 + 72x + 8y + 304 = 0.
a) Show that these two equations are equivalent.
b) When two equations are equivalent they have identical solution sets. Verify that the point (-12, -4) is a solution of both equations.
- If the equation Ax2 + By2 + Cx + Dy + F = 0 defines an ellipse, then what must be true about the values of the coefficients A and B?
- Explain why a circle is a special ellipse.
- An ellipse is formed when a double-napped cone is cut by a plane that cuts exactly one nap of the cone. Describe what happens to the ellipse as:
a) The plane gradually tilts towards being parallel to the generator of the double-napped cone.
| 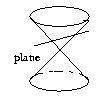 |
b) The plane gradually tilts towards being perpendicular to the vertical axis of the double-napped cone.
|
c) The plane cuts the cone exactly perpendicular to the vertical axis.
|
- The following ellipse is centred at (0, 0).
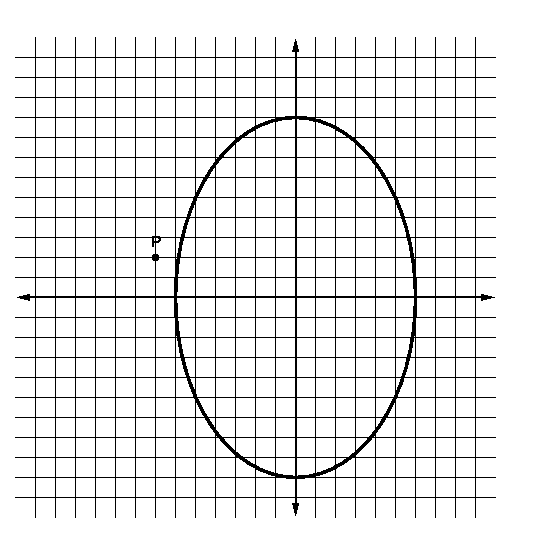
|
a) What are the lengths of the horizontal and vertical axes? |
horizontal |
_______________ |
vertical |
_______________ |
b) Write the standard equation of this ellipse. |
____________________________________ |
c) If the lengths of the axes remain the same, what would be the standard equation of this ellipse centred at the point P? |
____________________________________ |
d) Sketch the graph of the translated ellipse in the above graph paper.
e) Describe how the ellipse was translated.
|
|
|