| According to the Locus definition of an ellipse, the sum of the distances from any point, P, on the ellipse to each of the focal points, F1 and F2, is constant:
PF1 + PF2 = constant
where PF1 is the notation for the length of the line segment connecting points P and F1. |
| The point P could be at any point on the ellipse, but let's consider the case when P equals A1, where A1 is the rightmost endpoint of the horizontal axis. |
PF1 + PF2 = A1F1 + A1F2 |
Let A2 be the leftmost endpoint of the horizontal axis. Then, by symmetry of the ellipse, A1F1 = A2F2.
Thus, we can rewrite the statement as: |
A1F1 + A1F2 = A2F2 + A1F2 |
| But A2F2 + A1F2 is actually the entire horizontal axis. Therefore: | A2F2 + A1F2 = A1A2 = 2a |
| By definition, we knew that the sum of the distances from any point P to each of the focal points was a constant, but now we know even more. The sum of these distance always equals 2a, the length of the horizontal axis. |
| |
Now, by cleverly choosing P as another special point on the ellipse we can get closer to showing our aim, finding an equation for the locations of the focal points.
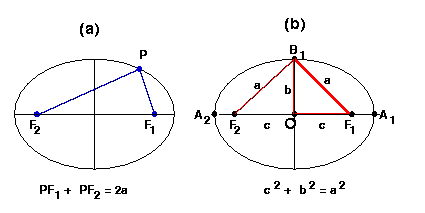
| Let P be located at the endpoint of the vertical axis, at the point B1. (See Figure 1(b)) |
PF1 + PF2 = B1F1 + B1F2 |
| By symmetry, the triangle B1F1F2 is an isocoles triangle. Therefore, B1F1 = B1F2 Thus: |
B1F1 + B1F2 = 2 B1F1 |
| As shown above, this sum must equal 2a, so: |
2 B1F1 = 2a |
| Divide both sides by 2: |
B1F1 = a = B1F2 |
| We now know that the length from the end of the vertical axis to either focal point is a. | |