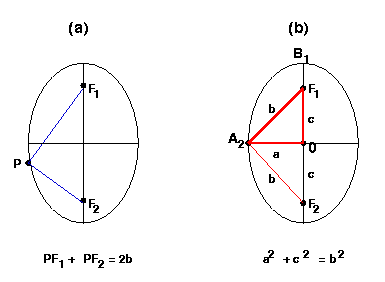
| Recall from page 2b.1 that when the horizontal axis was longer than the verticle axis, the sum of the distances between any point on the ellipse, P, and each of the foci was equal to the length of the major axis, 2a. |
| In the case we are now considering, the vertical axis fo the ellipse is longer than the horizontal axis. It can be shown that in this case, the sum of the distances from point P to each focal point is 2b, the length of the vertical axis. |
| Now let P be the left endpoint of the horizontal axis, the point A2. |
PF1 + PF2 = A2F1 + A2F2 |
| By symmetry, the triangle A2F1F2 is an isocoles triangle. Therefore, A2F1 = A2F2 Thus: |
A2F1 + A2F2 = 2 A2F1 |
| As shown above, this sum must equal 2b, so : | 2 A2F1 = 2b |
| Divide both sides by 2: |
A2F1 = b |
| So now we know that the distance from the end of the vertical axis to either focal point is b. |