| After completing this module you will be able to: |
- Describe that a parabola has a vertex and one axis of symmetry.
|
- Describe that the equation Ax2 + By2 + Cx + Dy + F = 0 represents a parabola when A = 0, B
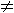 0 and C 0 and C 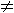 0; or B = 0, A 0; or B = 0, A 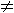 0 and C 0 and C 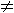 0. 0.
|
- Write the general equation of a parabola not centred at the origin as
Ax2 + Cx + Dy + F = 0 when B = 0 or By2 + Cx + Dy + F = 0 when A = 0.
|
- Write the general equation of a parabola centred at the origin as Ax2 + Dy = 0 or By2 + Cx = 0.
|
- Rewrite an equation of the form Ax2 + By2 + Cx + Dy + F = 0 in the standard form.
|
- Write the standard equation of a parabola with vertex at any point (h, k) as y - k = a(x - h)2
or x - h = a(y - k)2.
|
- Show that the standard equation of a parabola can also be written as
y = a(x - h)2 + k or x = a(y - k)2 + h.
|
- Write the standard equation of a parabola centred at the origin as y = ax2
or x = ay2.
|
- Describe what the variables h, k and a represent in the standard equation of a parabola.
|
- Describe the effect that varying h, k and a in the standard equation has on the graph of a parabola.
|
- Identify the characteristics of a parabola given its standard equation.
|
- Write the standard equation of a parabola given its vertex and a value a that describes its shape.
|
- Rewrite an equation of a parabola from standard form to an equation of the form Ax2 + By2 + Cx + Dy + F = 0.
|
- Show that the standard equation of a parabola is equal to the general equation of a parabola.
|
- Describe what happens when a plane parallel to the generator cuts the
double-napped cone at various locations.
|