| Page 2 | PARABOLA Menu | MAIN MENU |
|
Writing the Equation of a Parabola in Standard Form when |
We know that when 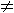 0 0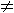 0 0 |
| Notice though, that the equation |
| How can we rewrite the equation |
| Just as with circles and ellipses, there is a standard equation for parabolas which provides useful information about their graphs. This equation looks like this: |
| As before, to change from general form to this new standard form, you will use a method called Completing the Square. |
| In the following examples we will use this method to rewrite equations from the form |
| Summary of Steps |
| STEP 1: | Collect like terms together.
| STEP 2: | Move constant terms to the right hand side of the equal sign.
| STEP 3: | Factor out the coefficient of x2 from each x term.
| Factor out the coefficient of y2 form each y term. STEP 4: | Complete the squares if necessary. Add numbers to both sides of the equation.
| STEP 5: | Simplify.
| STEP 6: | Divide and rearrange to get an equation of the form | NOTE: | If we are dealing with a parabola that has its vertex at the origin, we only need to use Steps 1 and 5. |
In the following questions, you will practise converting the equations of parabolas from general form to standard form.
| | |