[Back to the Cone Menu]
Print this quiz as a Word Document

Conic Sections Quiz: Double-Napped Cone Module
Name:___________________________________

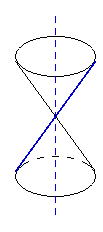
Instructions:Answer all the following questions in the space provided. Simplify all answers. Describe or show how a double-napped cone is created. Label the vertex, vertical axis, generators in the following diagram of a double-napped cone. a) Describe or show how the double-napped cone can be sliced to create circles. b) Describe what happens to a circle as the plane cutting the double-napped cone moves:      i) towards the cone's vertex      ii) away from the cone's vertex a) Describe or show how the double-napped cone can be sliced to create ellipses. b) Describe what happens to an ellipse as the plane cutting the double-napped cone gradually becomes:      i) more parallel to the cone's generator.      ii) more perpendicular to the cone's generator. a) Describe or show how the double-napped cone can be sliced to create hyperbolas. b) Describe what happens to a hyperbola as the plane cutting the double-napped cone moves:      i) closer to the cone's vertex.      ii) farther away from the cone's vertex. a) Describe or show how the double-napped cone can be sliced to create parabolas. b) Describe what happens to a parabola as the plane cutting the double-napped cone moves:      i) closer to the cone's vertex.      ii) farther away from the cone's vertex. a) Use the below chart to describe or show how the double-napped cone can be sliced to create each of the degenerate cases. Degenerate Conic Describe or show how this Degenerate Case is Created a point        a line        intersecting lines        State the general equation that describes all the conic sections and degenerate conics algebraically.