 |
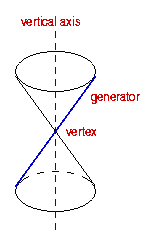
The double-napped cone has several important parts known as the generator, vertex and vertical axis. These parts are labeled on the diagram to the left.
When a double-napped cone is sliced into sections by a plane, curves known as the conic sections or conics are formed.
There are four conic sections : the circle, the ellipse, the hyperbola, and the parabola.
Slicing the double-napped cone can also result in the formation of a point, a straight line, or a pair of straight lines. These geometric figures are called the degenerate conics.
The type of conic section or degenerate conic that is formed depends on how and where a plane slices the double-napped cone.
In the following module, you will learn how to slice the double-napped cone to create each of the four conic sections and each of the three degenerate conics.
| Before you start, print off the Notes to keep you on task page. As you work through this module, fill in the blanks. At the end, you will then have some brief notes to study from.
| | | | | | |

