Extensions Page 1b.1

Page 1b.1

Rotation of a Point by 45^o

We want to find out how the coordinates of a point are changed when it is rotated by 45^o about its origin in a counter-clockwise direction.
Suppose that P is a point with coordinates 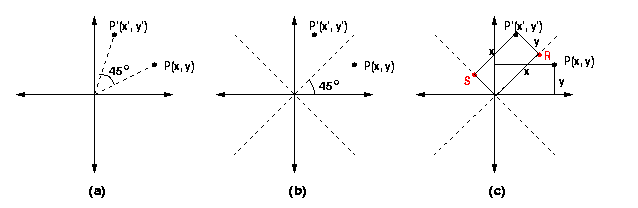(x, y) and that P', a point with coordinates (x', y'), is the new location of P after rotation by 45^o. (see Figure 1(a))
Figure 1

Figure 1(b) shows P and P' and a new set of "axes" rotated 45^o with respect to the original axes.
In Figure 1(c), perpendicular lines are dropped from P to the x and y-axes and perpendiculars are dropped from P' to the rotated axes, hitting them at points R and S as shown.
You can see that R is located a distance x from the origin along the straight line of slope 1. So the coordinates of R are (x/ Ö2 , x/ Ö2 ). Likewise, the coordinates of S are (-y/ Ö2 , y/ Ö2 ).
The location of P' can now be found by coordinatewise (or vector) addition.
That is:

(x', y') = ( x , x ) + ( -y, y ) = ( x - y, x + y )
Ö2 Ö2 Ö2    Ö2 Ö2    Ö2

So,
x' = (x - y)
      Ö2
y' = (x + y)
      Ö2