Page 1b

EXTENSIONS Menu

MAIN MENU

Suppose we went to find an equation for an ellipse whose axes of symmetry are not horizontal or vertical, but are tilted with respect to the x and y-axes.

In general, the computations are quite involved so we content ourselves with working out one example in detail.

EXAMPLE
Consider the ellipse E1 shown in Figure 1. Its major axis has length 4 and lies along the line 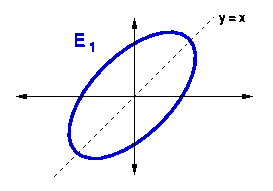y = x; its minor axis has length 2 and its centre is at the origin.
Figure 1
We can start with a congruent ellipse with centre at the origin and major axis along the x-axis as in Figure 2.
Figure 2
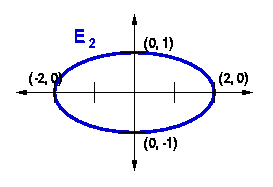
In standard form, the equation of the ellipse E2 is:  x2 + y2 = 1 22
In general form, this equation becomes: x2 + 4y2 - 4 = 0
Now we want to rotate E2 by 45o in a counter-clockwise direction to get E1. Any point (x, y) on E2 moves to a new point (x', y') on E1, where x' = (x - y) and Ö2 y' = (x + y)        Ö2
Check out a derivation of these marvelous relations.
To find out what equation the point (x', y') satisfies, you need to convert the x and y in x2 + 4y2 - 4 = 0 (the equation of E1) into x' and y'. So you need expressions of x' and y'. This is easy: x' = (x - y)       (1) Ö2     y' = (x + y)        (2) Ö2      Add (1) and (2): x' + y' = 2x = Ö2 x   Ö2 Thus x = (x' + y')        (3) Ö2      Subtract (1) from (2) y' - x' = 2y = Ö2y     Ö2 Thus y = (y' - x')        (4) Ö2
Now substitute (3) and (4) into the equation for E2: x2 + 4y2 - 4 = 0 ==> [(x'+ y')/ Ö2 ]2 + 4[(y' - x')/ Ö2 ]2 - 4 = 0 ==> (x'2 + 2x'y' + y'2)/ 2 + 2(y'2 - 2x'y' + x'2) - 4 = 0 ==> x'2 + 2x'y' + y'2 + 4y'2 - 8x'y' + 4x'2 - 8 = 0 ==> 5x'2 + 5y'2 - 6x'y' - 8 = 0
Now, (x', y') was just an arbitrary point on E2, so the variable notation can be changed. Thus E1 is the set of all points (x, y) such that 5x2 + 5y2 - 6xy - 8 = 0.

The action figure below allows you to change A, B, C, D, E and F to show the graph of Ax2 + By2 + Cx + Dy + Exy + F = 0. The ellipse E1 appears or disappears when you click on the blue button. Create a red graph of the equation 5x2 + 5y2 - 6xy - 8 = 0 to check our work. It is most interesting to watch if you use the arrows to click F to -8 first, followed by E to -6, A to 5 and then B to 5.

If all was done correctly, the red ellipse should cover the blue ellipse.