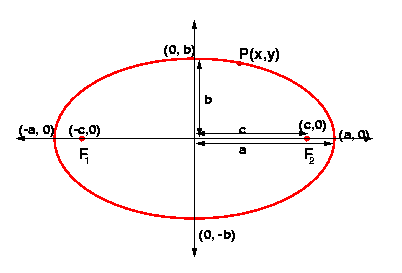Page 2c.2

EXTENSIONS Menu

MAIN MENU

First we will consider deriving the standard equation using PF1 + PF2 = 2a	FIGURE 1
Let's draw a general diagram of an ellipse centred at the origin, and label some important points and distances.
Using the distance formula, you can find the length of PF1 using the points (-c, 0) and P(x, y). PF1 = [(x + c)2 + y2]½
Similarly, the length of PF2 can be found using the points (c, 0) and P(x, y). PF2 = [(x - c)2 + y2]½
Using these two pieces of information, we have: PF1 + PF2 = 2a [(x + c)2 + y2]½ + [(x - c)2 + y2]½ = 2a Isolate one of the radicals: [(x + c)2 + y2]½ = 2a - [(x - c)2 + y2]½ Square both sides: (x + c)2 + y2 = 4a2 - 4a[(x - c)2 + y2]½ + (x - c)2 + y2 Expand: x2 + 2cx + c2 + y2 = 4a2 - 4a[(x - c)2 + y2]½ + x2 - 2cx + c2 + y2 Isolate the radical: 4a[(x - c)2 + y2]½ = 4a2 - 4cx Divide by 4: a[(x - c)2 + y2]½ = a2 - cx Square both sides: a2[(x - c)2 + y2] = a4 - 2a2cx + c2x2 Expand: a2(x2 - 2cx + c2 + y2) = a4 - 2a2cx + c2x2 a2x2 + a2c2 + a2y2 = a4 + c2x2 Rewrite equation as: (a2 - c2)x2 + a2y2 = a2(a2 - c2) Recall from the Pythagorean Property that a2 - c2 = b2. Make this substitution: b2x2 + a2y2 = a2b2 Divide both sides by a2b2: x2/a2 + y2/b2 = 1 This is the standard equation of an ellipse centred at the origin.
We can also derive the standard equaion of an ellipse centred at the origin using the locus definition: PF1 + PF2 = 2b.
Try doing this on your own by drawing a diagram and using the steps in the previous proof as a guide.