Page 2c

EXTENSIONS Menu

MAIN MENU

Historically, the Greeks only knew the locus definition of an ellipse.		DESCARTES
In later years, Decartes put the ellipse on the coordinate plane with its centre at the origin, and found that he could use the locus definition to find the standard equation of an ellipse.
Let's look at a diagram to see how this can be done.
Notice in Figure 1 that F1 and F2 are the focal points of the ellipse and P is any point on the ellipse.
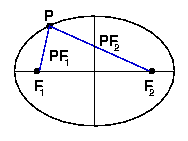Figure 1	Using these distances and the locus definition, you know that PF1 + PF2 = constant value.
	You can prove that when the horizontal axis is longer than the vertical axis of the ellipse, PF1 + PF2 = 2a, where 2a is the length of the horizontal axis.
Proof of PF1 + PF2 = 2a
Similarly, you can prove when the vertical axis is longer than the horizontal axis of the ellipse, PF1 + PF2 = 2b, where 2b is the length of the vertical axis.
Using these equations you can derive the standard equation of any ellipse.

In general, you can use the same procedure to derive the standard equation of any ellipse.

Check out the general derivation of the standard equation,  x2/a2 + y2/b2 = 1, using the locus definition.